ΠΑΡΑΓΩΓΟΙ

 

Ποια είναι η χρήση των παραγώγων στην Φυσική και τι ακριβώς είναι; Ένα παράδειγμα θα μας διαφωτίσει. Έστω ότι ένα αυτοκίνητο βρίσκεται την χρονική στιγμή t = 0 s στο σημείο x = 0 m και κινείται σε ευθύγραμμη ομαλή κίνηση με ταχύτητα u = 2 m/s. Αυτό σημαίνει ότι σε ίσα χρονικά διαστήματα, διανύει ίσες αποστάσεις, επομένως το διάγραμμα x-t πρέπει να είναι μια ευθεία γραμμή:

 

Σχήμα 1

 

Για να υπολογίσουμε την ταχύτητα π.χ. στο t = 4 s χρησιμοποιούμε την γνωστή σχέση x/t εάν ξεκινάμε από το x, t = 0, 0 όπως σε αυτό το παράδειγμα. Αυτό δίνει

 

x/t = 8m / 4s = 2 m/s   

 Αυτή είναι και η κλίση της ευθείας του γραφήματος. Τι γίνεται όμως στην πεπίπτωση ενός τρελού οδηγού που αυξομειώνει την ταχύτητά του; Θεωρήστε για παράδειγμα τα δεδομένα που κατέγραψε ένας φοιτητής ως συνοδηγός στο αυτοκίνητο ενός φίλου του στον δρόμο μπροστά από την πρυτανεία:

Σχήμα 2

 

Από την αρχική κλίση φαίνεται ότι ο οδηγός ξεκίνησε με μεγάλη ταχύτητα στο t = 0 (κόντρα;) αλλά μετά ελάττωσε ταχύτητα γιατί συνειδητοποίησε ότι δεν είναι σωστό αυτό που κάνει λόγω ασφαλείας αλλά και λόγου του υπερβολικού θορύβου που κάνει η εξάτμισή του! Περνώντας από το περίπτερο στο x = 80m σταμάτησε για περίπου 2 δευτερόλεπτα (τμήμα ΑΒΓ) να ρωτήσει εάν υπάρχουν αθλητικές εφημερίδες (μπορείτε να μαντέψετε την απάντηση;). Μετά συνέχισε πάλι την πορεία του αυξομειώνοντας την ταχύτητά του για να προσαρμοσθεί στις ανάγκες της κυκλοφορίας. Προφανώς η κίνηση του δεν είναι ευθύγραμμη ομαλή αφού για ίδια χρονικά διαστήματα βρίσκουμε διαφορετικούς χρόνους (αυτό φαίνεται από το διάγραμμα εάν σχηματίσουμε τρίγωνα παρόμοια με αυτά του Σχήματος 1 σε διαφορετικά σημεία).   Η ερώτηση είναι πως μπορούμε να υπολογίσουμε τώρα την ταχύτητα σε διαφορετικά σημεία της καμπύλης. Εάν χρησιμοποιήσουμε την γνωστή μας έκφραση x/t θα μας δώσει λάθος αποτελέσματα αφού π.χ. στο σημείο Β δίνει

 

x/t = 80m / 4s = 20 m/s           

 

(αυτή είναι η κλίση της ευθείας ΟΒ αλλά δεν έχει σχέση με την ταχύτητα). Διαισθητικώς περιμένουμε ότι σε σημεία με μεγάλη κλίση να έχουμε και μεγάλη ταχύτητα γιατί μεγάλη  κλίση σημαίνει ραγδαία αύξηση του x για μικρές μεταβολές του t.

 

Πως όμως υπολογίζουμε την κλίση μιας καμπύλης; Ας ξεκινήσουμε από αυτά που ήδη γνωρίζουμε: Η κλίση μιας ευθείας μεταξύ δύο σημείων Α(tA, xA) και Β(tΒ, xΒ) δίνεται από την έκφραση

 

λ = (xΒ - xA) / (tΒ - tA)             (1)

 

Η παραπάνω έκφραση μπορεί να χρησιμοποιηθεί εάν κοιτάξουμε μια καμπύλη “σε μικροσκόπιο”. Τότε σε μικρά διαστήματα η καμπύλη δεν αλλάζει απότομα και μπορούμε να την θεωρήσουμε ως σύνολο πολύ μικρών ευθύγραμμων τμημάτων. Θεωρήστε για παράδειγμα το παρακάτω διάγραμμα (προσέξτε πόσο μικρές είναι οι μονάδες):

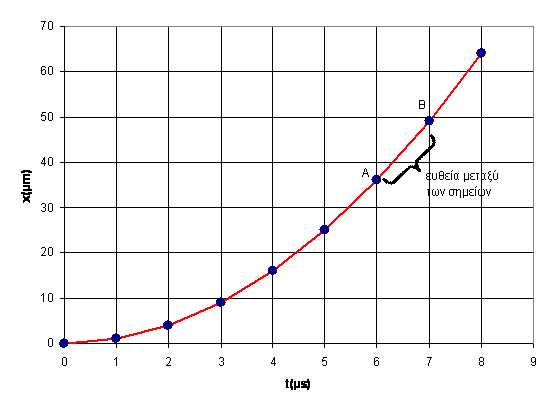Σχήμα 3

 

Εδώ τα μπλε σημεία ανήκουν σε μια καμπύλη και ενώνονται μεταξύ τους με τα κόκκινα ευθύγραμμα τμήματα (όπως το ΑΒ). Προσέξτε ότι τα τμήματα ως σύνολο μοιάζουν να είναι η καμπύλη και δύσκολα μπορεί να διακρίνει κανείς την διαφορά. Επομένως έχει νόημα να πούμε ότι η κλίση της καμπύλης σε ένα σημείο είναι κατά προσέγγιση ίση με την κλίση του αντίστοιχου ευθύγραμμου τμήματος και να χρησιμοποιήσουμε την σχέση (1) παραπάνω. Π.χ. στο σημείο Α η κλίση είναι

 

λ = (49-36 μm) / (7-6 μs) = 13 m/s     

 

Πόσο ακριβής είναι αυτή η κλίση; Όσο μικρότερο το ευθύγραμμο τμήμα τόσο το καλύτερο. Εάν για παράδειγμα χωρίζαμε το παραπάνω διάγραμμα ανά Δt = 1 ns αντί για Δt = 1 μs, τότε τα ευθύγραμμα τμήματα θα ήταν σχεδόν σαν μια συνεχόμενη καμπύλη. Εάν λοιπόν γράφαμε ένα πρόγραμμα στον υπολογιστή και χρειαζόταν να υπολογίσουμε την κλίση μιας καμπύλης σε κάθε σημείο, τότε θα κατασκευάζαμε έναν βρόγχο (loop) με μικρό βήμα dt = 1E-10 s και θα χρησιμοποιούσαμε την παραπάνω σχέση. Μαθηματικώς όταν κάτι γίνεται μικρότερο και μικρότερο λέμε ότι παίρνουμε το όριο του στο μηδέν. Έτσι η πιο ακριβής γραφή της εξίσωσης (1) θα ήταν

 

                                               

 

Τώρα εάν διαλέξουμε για tA μια τυχαία χρονική στιγμή t τότε το tΒ = tA + Δt. Εάν το x είναι μια συνεχής συνάρτηση του t, δηλαδή x(t), τότε η κλίση την χρονική στιγμή t δίνεται από την

                                          

 

Αυτή η έκφραση είναι ο ορισμός της παραγώγου στα Μαθηματικά. Μπορεί να φαίνεται κάπως αφηρημένη έννοια αλλά για δεδομένο αριθμό t μας δίνει έναν άλλο αριθμό που εκφράζει την κλίση της καμπύλης  x(t) στο συγκεκριμένο t. Επειδή γενικά μια καμπύλη  δεν έχει σταθερή κλίση, τότε η παράγωγος είναι μια νέα συνάρτηση f(t), δηλαδή

                                                                             (2)

 

Ευτυχώς για εμάς, δεν χρειάζεται να καθόμαστε να υπολογίζουμε την (2) για κάθε γνωστή συνάρτηση  x(t) αφού το έχουν κάνει ήδη οι Μαθηματικοί για εμάς. Για παράδειγμα η παράγωγος ορισμένων γνωστών συναρτήσεων φαίνονται στον παρακάτω πίνακα:

 

x(t)

f(t)

t

1

tn

ntn-1

ln t

1/t

sin(t)

cos(t)

cos(t)

-sin(t)

et

et

 

Πίνακας 1
Επίσης οι Μαθηματικοί μας έχουν δώσει και ένα σύνολο κανόνων για τον υπολογισμό των παραγώγων των πιο σύνθετων συναρτήσεων (ο φοιτητής παραπέμπεται σε βιβλία Μαθηματικής Ανάλυσης) . Οι δε Φυσικοί κουράζονται να κουβαλάνε συνεχώς τον ορισμό του ορίου διότι οι παράγωγοι εμφανίζονται τακτικώς στην Φυσική και έτσι χρησιμοποιούν τον λεγόμενο “απειροστό χρόνο” dt και την “απειροστή απομάκρυνση” dx οι οποίοι ορίζονται ως  και αντίστοιχα. Έτσι  η παράγωγος (2) παίρνει την εξής απλή μορφή

 

                                                                                                         

 

Αυτός ο ορισμός δίνει μια κάπως πιο καθαρή φυσική εποπτεία αφού μας θυμίζει ότι τα dt και dx δεν είναι τίποτα άλλο από μικρές μεταβολές (ονομάζονται επίσης και διαφορικά) και ο λόγος τους είναι κάτι σαν ρυθμός. Έτσι η ταχύτητα στην Φυσική συμβολίζεται ως , η επιτάχυνση , η γωνιακή ταχύτητα και η ισχύς (έργο ανά μονάδα χρόνου). Η παράγωγος της παραγώγου, δηλαδή η δεύτερη παράγωγος, συμβολίζεται ως

                                                    

(προσέξτε την θέση του τετραγώνου στον κάθε όρο).

 

Παράδειγμα 1. Να υπολογισθεί η ακριβής κλίση του x(t) στο σημείο Α του Σχήματος 3. Λύση:

 

Με μια γρήγορη ματιά μπορούμε να δούμε ότι τα σημεία επαληθεύουν την καμπύλη x(t) = t2 όπου το x είναι σε μm και το t είναι σε μs. Η  κλίση σε κάθε σημείο είναι        λ = dx/dt και σύμφωνα με τον Πίνακα 1 έχουμε λ = 2t. Στο σημείο Α ο χρόνος είναι    t = 6 μs και άρα  λ = 12 m/s. Να συγκριθεί αυτό με την τιμή των 13 m/s που βρέθηκε παραπάνω. 

 

Παράδειγμα 2. Ένα κινητό κινείται σύμφωνα με την σχέση x(t) = cos(t). Ποια είναι η θέση του και η ταχύτητά του στο σημείο t = 0; Λύση:

 

Η θέση του είναι x(0) = cos(0) = 1. Από τον Πίνακα 1 η ταχύτητα του είναι                         u = dx/dt = sin(t) και στο t = 0 έχουμε u(0) = 0.

 

 

Σημείωση: Ο συμβολισμός παριστάνει την μερική παράγωγο (δες Παράρτημα 2)

 

 

Δ. Κουζούδης

 

 

 

 

ΑΟΡΙΣΤΑ ΟΛΟΚΛΗΡΩΜΑΤΑ

 

Το αόριστο ολοκλήρωμα είναι απλά το αντίθετο της παραγώγου. Έτσι εάν π.χ. η F(t) είναι η παράγωγος της  f(t)  (δηλαδή F = df / dt) τότε η f(t)  είναι το αόριστο ολοκλήρωμα της F(t). Για να βρούμε τα αόριστα ολοκληρώματα γνωστών συναρτήσεων απλά καταφεύγουμε στον Πίνακα 1 και αντιστρέφουμε τις στήλες του.

 

Έτσι το αόριστο ολοκλήρωμα της συνάρτησης  1/t είναι το ln t κ.ό.κ. Γεωμετρικώς αυτό ισοδυναμεί με την ερώτηση ποια συνάρτηση στο σημείο t έχει κλίση ίση με 1/t; Απάντηση: Η συνάρτηση f(t) = ln t. Βέβαια για να είμαστε απολύτως ακριβείς πρέπει να προσθέσουμε και μια αυθαίρετη σταθερά, δηλαδή το αόριστο ολοκλήρωμα του 1/t είναι το ln t + c όπου c είναι μια αυθαίρετη σταθερά. Αυτό γίνεται γιατί εάν μετατοπίσουμε μια καμπύλη κατά c, η κλίση της δεν αλλάζει. Επομένως η οικογένεια καμπυλών ln t + c έχουν όλες τις ίδια κλίση για δεδομένο t.

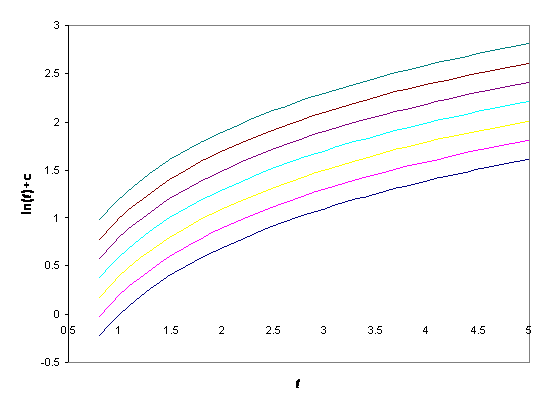Σχήμα 4

 

Αυτό που κάπως μπερδεύει τους φοιτητές είναι ο συμβολισμός του ολοκληρώματος. Αυτό που λέμε με λόγια ότι η f(t) είναι το αόριστο ολοκλήρωμα της F(t), το γράφουμε μαθηματικώς ως

                                                        

Π.χ.     

δηλαδή χρησιμοποιούμε μια ειδική καμπύλη (κάτι σαν Αγγλικό S τραβηγμένο) αλλά στο τέλος βάζουμε το διαφορικό της μεταβλητής ως προς την οποία ολοκληρώνουμε. Γιατί γίνεται αυτό θα το καταλάβουν οι φοιτητές εν καιρώ (εγώ ακόμα προσπαθώ!!! Αστειεύομαι φυσικά). Για τώρα απλά χρησιμοποιείστε τον συμβολισμό αυτόν τυφλά ή διαβάστε το Παράρτημα 1 στο τέλος αυτών των σημειώσεων για μια καλύτερη εξήγηση.

 

Παράδειγμα 3. Ένα κινητό κινείται σύμφωνα με ταχύτητα u που δίνεται από την σχέση u(t) = t3. Ποια είναι η έκφραση της θέση του x(t) συναρτήσει του χρόνου; Λύση:

 

Αφού u = dx/dt τότε αντιστρόφως . Σύμφωνα με τον Πίνακα 1 εάν παραγωγίσω το t4 παίρνω 4 t3, άρα το αόριστο ολοκλήρωμα του 4t3 είναι το t4. Οι Μαθηματικοί μας λένε ότι η πράξη της παραγώγισης δεν επηρεάζει τις πολλαπλασιαστικές σταθερές οπότε διαιρώ με 4 και έχω ότι το αόριστο ολοκλήρωμα του t3 είναι το t4/4.   Επομένως

Προσέξτε ότι συμπεριλήφθηκε και η σταθερά c. Αυτή η αυθαίρετη σταθερά γίνεται συγκεκριμένη εάν μας δοθούν αρχικές συνθήκες, π.χ. εάν το σώμα στο t = 0 ξεκινάει από την αρχή των αξόνων x = 0, τότε από την παραπάνω εξίσωση έχουμε και c = 0.

 

 

 

Δ. Κουζούδης

 

 

 

 

 

 

ΟΡΙΣΜΕΝΟ ΟΛΟΚΛΗΡΩΜΑ

 

ΟΡΙΣΜΟΣ: Το ορισμένο ολοκλήρωμα είναι η διαφορά του αορίστου ολοκληρώματος σε δυο διαφορετικά σημεία t1 και t2. Συμβολίζεται ως εξής:

 

                                                             

 

Έτσι εάν η f(t) είναι το αόριστο ολοκλήρωμα της F(t), τότε

 

                                                 

 

Σημείωση: Ορισμένες φορές την διαφορά την συμβολίζουμε ως

 

Για παράδειγμα το ορισμένο ολοκλήρωμα

 

                                                                

ισούται με .

 

Παρατηρήστε ότι αντίθετα με το αόριστο ολοκλήρωμα που είναι μια συνάρτηση, το ορισμένο ολοκλήρωμα είναι ένα απλός αριθμός. Επίσης η αυθαίρετη σταθερά c του αορίστου ολοκληρώματος απαλείφεται λόγω της διαφοράς, οπότε μπορούμε εξ’αρχής να την παραλείψουμε στην .

 

 

Δ. Κουζούδης

 

 

 

Παράρτημα 1: Ο συμβολισμός του ολοκληρώματος

 

 

Γιατί εισάγουμε ένα διαφορικό dt μέσα στον συμβολισμό του ολοκληρώματος; Ιδού δυο εξηγήσεις:

 

α) Όπως είδαμε ο συμβολισμός  σημαίνει ότι η f(t) είναι το αόριστο ολοκλήρωμα της F(t), ή αντίστροφα η F(t) είναι η παράγωγος της f(t):

 

                                                                    

Συνδυάζοντας τις δυο έχουμε

 

 

Αυτό σημαίνει ότι η πράξη της ολοκλήρωσης  αναιρεί  την πράξη της διαφόρισης d , η οποία όπως είπαμε περιορίζει κάτι στο όριο του μηδενός. Εξ ου και η λέξη ολοκλήρωση που δηλώνει το αντίθετο.

 

β) Η φυσική σημασία του ορισμένου ολοκληρώματος είναι ότι το A ισούται με το εμβαδόν ανάμεσα στην καμπύλη g(x) και τον άξονα x μεταξύ των ορίων x1 και x2:

 

 

 

 

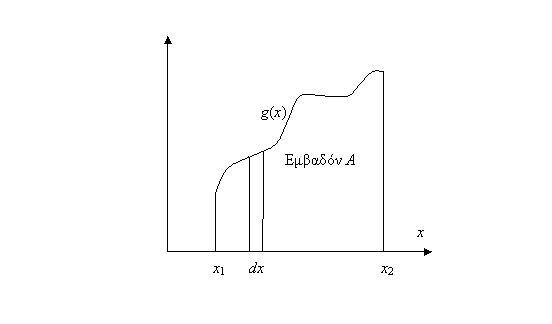
Οπότε η ιδέα είναι ότι σε ένα απειροστά μικρό διάστημα dx το g(x) είναι περίπου σταθερό και μας δίνει το ύψος του στοιχειώδους παραλληλογράμμου που φαίνεται στο παραπάνω σχήμα. Έτσι το  g(x)dx μας δίνει το εμβαδόν αυτού του παραλληλογράμμου (ύψος × βάση). Η ολοκλήρωση σημαίνει ότι παίρνουμε το σύνολο όλων των στοιχειωδών παραλληλογράμμων από x1 έως και  x2.

 

 

Δ. Κουζούδης

 

 

 

 

Παράρτημα 2: Η μερική παράγωγος

 

Όταν μια συνάρτηση έχει περισσότερες της μια μεταβλητές π.χ.  f = f(x, t) τότε έχει νόημα να παραγωγίσουμε ξεχωριστά την κάθε μια μεταβλητή, κρατώντας τις άλλες μεταβλητές σταθερές. Αυτές οι παράγωγοι ονομάζονται μερικές παράγωγοι, συμβολίζονται με και , και ισούνται με

 

                                            

                                            

 

 

Παράδειγμα: Εάν  f(x, t) = t3 ln(x)  τότε

 

 και

 

Δηλαδή παραγωγίζουμε την κάθε μεταβλητή ξεχωριστά ωσάν η άλλη μεταβλητή να ήταν μια σταθερά. 

 

 

Δ. Κουζούδης